Simple Q Learning 기법(Table) 소개
그렇다면 강화 학습을 프로그램으로 구현하기 위해서는 어떻게 해야 할까요? 위의 실습에서 Open AI Gym 프로즌 레이크 게임을 예로 들어 보겠습니다. 위의 게임에서는 현재 상태와 맵 정보, 골은 어디에 있고 어디가 함정인지 모두 알고 있는 상태에서 시작했습니다.
하지만 실제 게임에서는 전혀 다른 이야기가 됩니다. 이유는 현재 맵 정보를 알지 못하기 때문입니다. 현재 상태에서 어떤 액션을 취했을때 그곳이 보상을 받을수 있는 골 지점인지, 또는 그냥 길인지, 아니면 게임을 종료시키는 함정인지 알 방법이 없습니다.
여기서 Q가 등장합니다. 위에서 강화학습은 주어진 환경, 상태에서 액션을 취해 환경을 변화시키고 그것에 대한 보상으로 학습을 한다고 했습니다. 만일 이미 상태에 따라 여러가지 액션을 취해보고 그에 따른 결과(보상)를 알고 있는 존재가 있다면 어떨까요?
만약 그런 존재가 있다면 쉽게 목적지까지 도달 할 수 있을 것입니다. Q 라는 존재에게 현재 상태와 액션을 알려주고, 액션 중 가장 보상이 큰 행동을 취하면 될 것이기 때문입니다.
위에서 설명한 것처럼 Q는 현재상태에서 어떤 액션을 취했을때 보상이 어느정도 되는지 돌려주는 존재입니다. 즉 Q 란 다음과 같은 기능을 제공한다고 볼 수 있습니다.
현재 상태에서 특정 액션을 취했을때 기대되는 보상을 알려주는 기능 -> maxQ(상태, 액션)
현재 상태에서 가장 보상이 높은 액션을 알려주는 기능 -> argmaxQ(상태, 액션)
위에 기능을 구현하기 위하여 Q 는 Q 테이블을 사용합니다. Q 테이블은 각 상태에서 취할수 있는 모든 액션들의 기대보상을 가지고 있습니다. 그리고 액션을 취하다 보면 어느순간 보상이 있는 상태에 도달하게 될 것입니다. 이때 직전 상태에서 취한 액션의 기대보상을 Q 테이블에서 업데이트 하자는 것이 기본적인 아이디어입니다.
이해를 돕기위해 Frozen Lake 게임으로 Q 가 어떻게 동작하는지 예를 들어보겠습니다.
위 실습에서 게임을 진행해본 Frozen Lake 게임은 16개의 상태가 있습니다. 각 상태를 테이블처럼 표현하면 다음과 같이 될 것입니다.

여러가지 방법으로 각 상태에 대한 보상을 줄수 있지만 여기서는 단순하게 생각하기 위해 골(목적지) 상태는 보상을 1로 하고 나머지 상태는 보상을 0으로 해보겠습니다. 그것을 그림으로 보면 다음과 같이 됩니다.
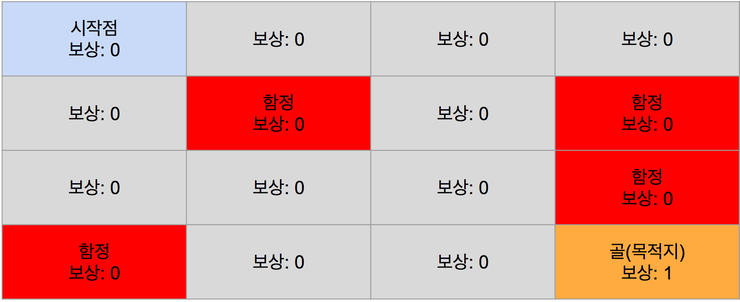
각 상태에서는 4가지 액션을 취할 수 있습니다. 그리고 Q 는 각 상태에서 취할수 있는 액션에 대한 기대 보상을 가지고 있다고 했습니다. 그것을 그림으로 그려보면 다음과 같이 될것입니다.

각 상태에서 취할수 있는 모든 액션에 대한 기대보상을 Q 는 위 그림과 같이 가지고 있습니다. 여기서 문제는 최초 게임이 시작되었을때는 Q 도 어디가 골이고 보상이 있는지 모른다는 것입니다.
따라서 최초에는 Q 테이블의 모든 값을 0 으로 초기화 합니다.

게임을 시작하고 꽤 오랫동안은 Q 테이블의 값이 모두 0이기 때문에 어디로 가는것이 최선인지 알려줄수가 없습니다. 그러므로 어느정도 기간은 아무 액션이나 랜덤하게 선택하여 환경을 변화시켜 보는 방법 밖에 없습니다.
만약 랜덤으로 선택한 액션이 시작점에서 오른쪽으로 간 뒤 아래쪽으로 가는 액션이면 어떻게 될까요?
- Right -> Down
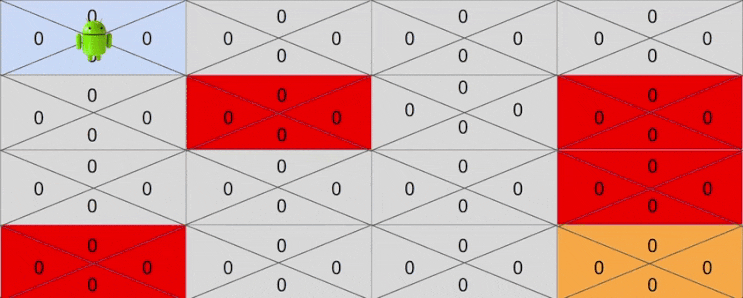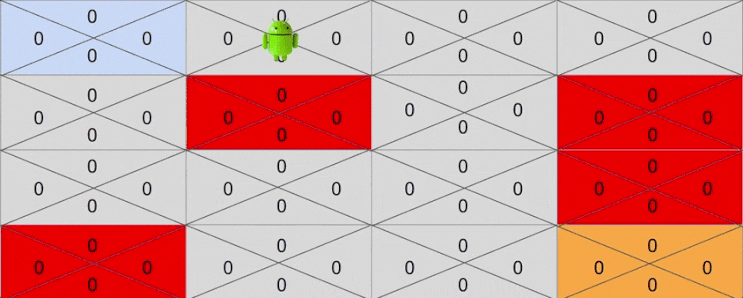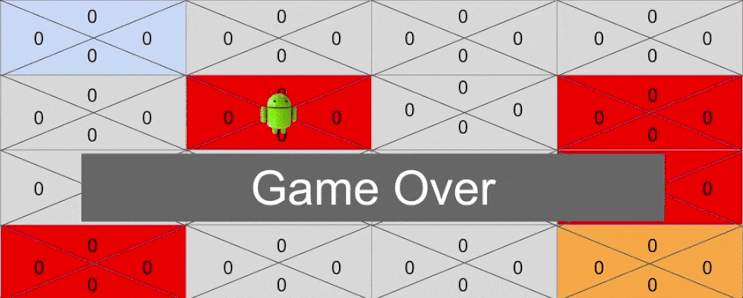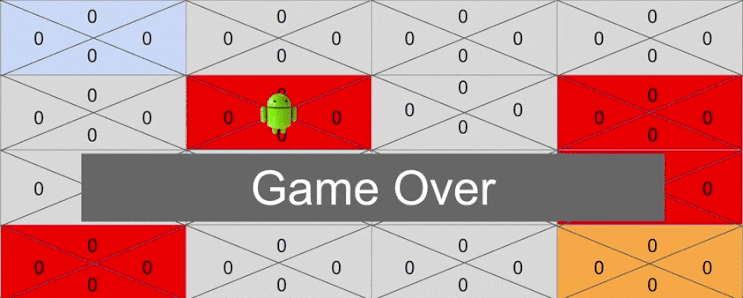
보상이 있는 상태까지 도달하지 못했기 때문에 모든 Q 테이블은 0 인 채로 게임이 종료되게 됩니다. 아무것도 변한것이 없는 것이죠. 즉 시행착오만 있었던 셈입니다.
하지만 어느순간 운이 좋게도 보상까지 도달하는 경우도 있을 것입니다. 이를테면 운이좋게 다음과 같이 액션을 취했다고 생각해봅시다.
- Right -> Right -> Down -> Down -> Down -> Right
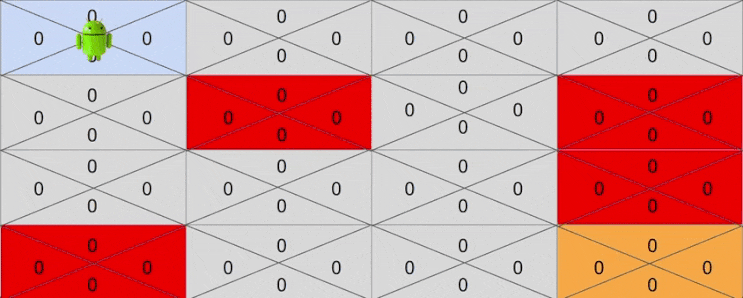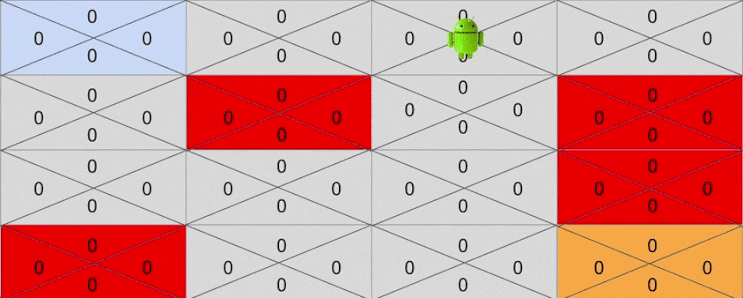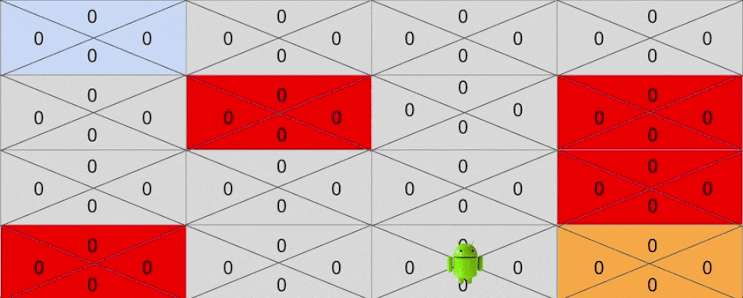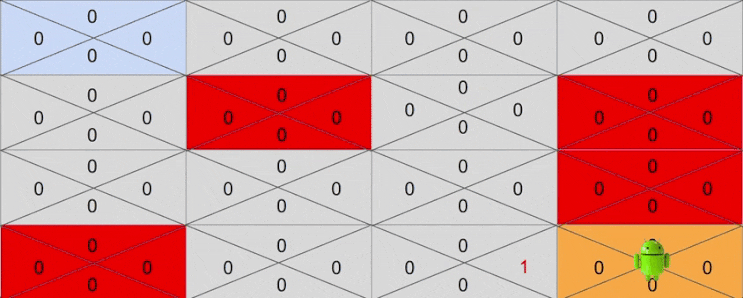
마지막 골에 도착한 후에 골 바로 이전 상태에서 Right 액션에 대한 기대보상이 1로 바뀐것에 주목해주세요. 이제 Q 는 4행 3열에 있는 상태에서 Right 액션을 취하면 보상이 1이 된다는 것을 드디어 알게 된 것입니다.
이제 4행 3열에 있는 상태까지만 어떻게든 도달할 수 있다면 Right 액션을 취하면 된다고 Q 가 알려줄 수 있게된 것입니다. 또 Q가 알려준대로 움직이면 골까지 이동할 수 있기 때문에 어떻게든 4행 3열까지만 도착하면 골까지 헤맬 필요가 없습니다.
그렇다는 이야기는 목적지를 골로 볼 필요 없이 4행 3열을 다음 목표로 봐도 될것입니다.
다시 시행착오를 반복하며 행동을 취하다보면 어느순간에 4행 3열에 해당하는 상태에 도달할 때가 있을 것입니다. 이를 테면 다음과 같은 액션을 취했다고 생각해보겠습니다.
- Down -> Down -> Right -> Right -> Down
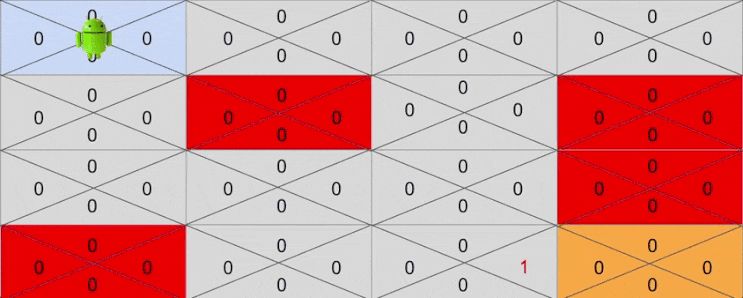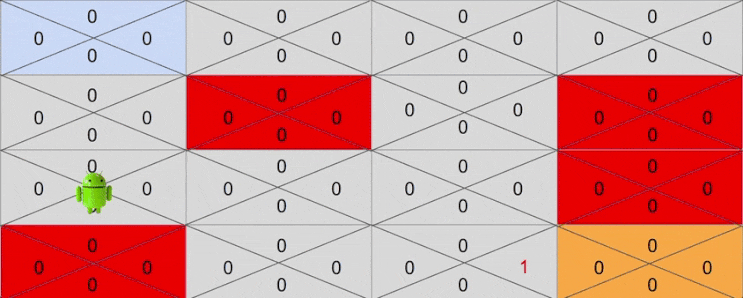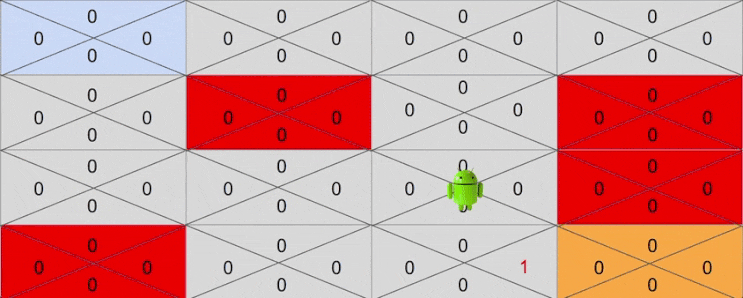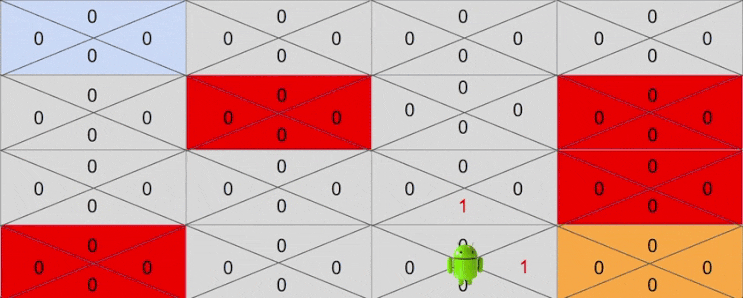
이번에는 4행 3열 이전 상태중 하나인 3행 3열에 Down 액션에 대한 기대보상이 1로 변하게 됩니다. 이제 목표 지점은 4행 3열이 아닌 3행 3열이 되겠죠.
이런식으로 랜덤하게 시행착오를 반복하다보면 어느순간에는 시작점부터 Q가 기대보상을 가지고 제대로 길안내를 하게 될 것입니다.
시행착오를 반복하면서 Q 테이블이 다음과 같이 업데이트 되었다고 가정하겠습니다.
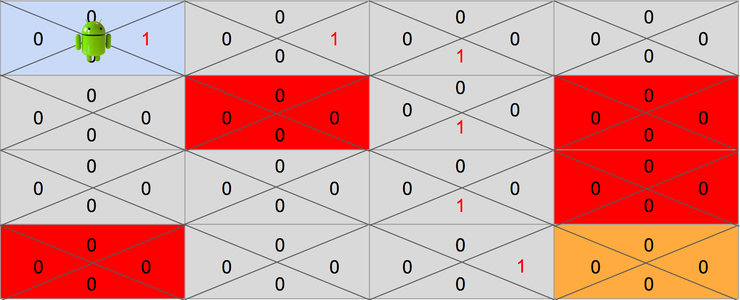
이제는 각 상태에서 어느쪽으로 가는게 최대보상인지 Q가 언제나 알려줄수 있습니다. 즉 길을 헤맬 이유가 없게 된것이죠. 지금까지 보아온 과정을 코드로 옮기기 위해서 동작과정을 정리하면 다음과 같습니다.
- Q 테이블을 0으로 모두 초기화
- 현재 상태에서 Q테이블의 액션 기대값중 가장 큰 액션 선택. 모든 액션의 기대값이 0 이라면 랜덤하게 액션 선택
- 현재상태에서 액션을 취해 환경을 변화시킴.
- 새로운 상태에서 보상이 있다면 현재상태에서 취한 액션에 기대보상을 업데이트.
- 새로운 상태를 현재 상태로 바꿈.
- 다시 2번 스텝부터 반복
위와 같이 Q 테이블이 업데이트 되는 과정을 수학적으로 한줄로 표현하면 다음과 같이 됩니다.
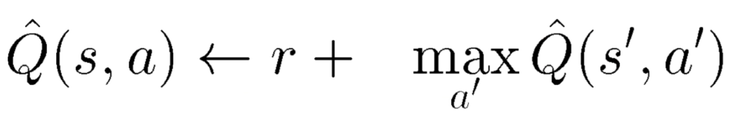
수학식으로 보면 상당히 난해하게 보일 수 있습니다. 이해하기 쉽게 한글로 보면 다음과 같습니다.
Q(상태, 액션) <- (액션을 취한 다음 상태의 보상) + (액션 후 다음 상태의 기대보상 중 최대값)
즉 현재의 Q 테이블의 액션에 대한 기대 보상을, 전달받은 액션을 취한뒤 다음 상태에서의 기대보상중 최대값으로 업데이트 한다는 이야기입니다.
이것을 실제로 코드로 작성하면 어떻게 되는지 다음 장에서 실습으로 확인하도록 하겠습니다.